Equações Polinomiais do 1º e 2º grau – Matemática Enem

Equações Polinomiais do 1º grau e 2º grau

Equação Polinomial do 1º grau

Equação é uma sentença matemática onde temos uma igualdade e envolve números desconhecidos representados por letras.

Temos que equação polinomial do 1º grau é toda equação que pode ser escrito na forma: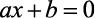

 Exemplos:

 a)

 b)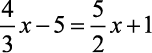

Equação Polinomial do 2º grau

Temos que equação polinomial do 2º grau é toda equação que pode ser escrita na forma:

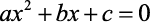
Raízes ou Zeros da Equação

É o valor numérico que, ao substituir a incógnita (letra que representa o valor desconhecido), torna a igualdade verdadeira.

Para o caso das equações polinomiais do 1º grau, temos:

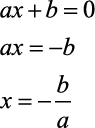
Para o caso das equações polinomiais do 2º grau, temos:

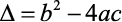
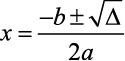
Exercício Resolvido

Encontrar a raiz das equações abaixo para U=Q.

a)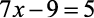

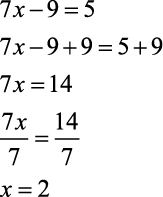
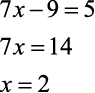
b)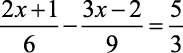

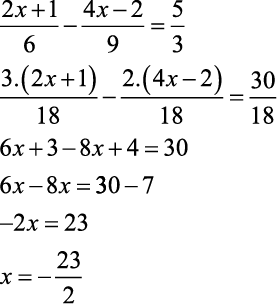
Questão 1. (Unisinos 2012) As soluções da equação

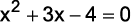
são

a) – 4 e -1.

b) – 4 e 1.

c) – 4 e 3.

d) – 1 e 3.

e) 1 e 3.

Resposta da questão 1: [B]

Basta aplicar a fórmula para a resolução da equação do 2º grau.

Portanto, as soluções são – 4 e 1.

Questão 2. (Ufsm 2011) Em uma determinada região do mar, foi contabilizado um total de 340 mil animais, entre lontras marinhas, ouriços do mar e lagostas. Verificou-se que o número de lontras era o triplo do de ouriços e que o número de lagostas excedia em 20 mil unidades o total de lontras e ouriços. Pode-se dizer que o número de ouriços dessa região é

a) 30 mil.

b) 35 mil.

c) 40 mil.

d) 45 mil.

e) 50 mil.

Resposta da questão 2:

[C]

Lontras: 3x

Ouriços: x

Lagostas 3x + x + 20.000

 3x + x + 3x + x + 20.000 = 340.000

8x = 320.000

x = 40.000

Saiba mais sobre Equações Polinomiais do  1º e 2º grau nesta aula do canal matematicaemexercicios.com, disponível no Youtube. Após assistir, revise o que você aprendeu respondendo aos nossos desafios!

Desafios

Questão 1

(G1 – ifsc 2011) A solução da equação tem como resultado,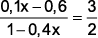

a) um número racional negativo.

b) um número irracional.

c) um número inteiro negativo.

d) um número racional maior que 5.

e) um número natural.

Dica 1 – Revise tudo sobre os Logaritmos em mais esta aula de Matemática Enem, com definições e exercícios resolvidos para você gabaritar no Exame Nacional do Ensino Médio – https://fuvestibular.com.br/logaritmos-matematica-enem-2/

Questão 2

(G1 – utfpr 2011) Se a e b são raízes da equação do segundo grau 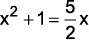, então a e b pertencem ao intervalo:

a) 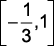b)

c) d)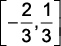

e)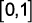

Dica 2 – Pronto para o Exame Nacional do Ensino Médio? Revise tudo sobre Função Exponencial em mais esta aula preparatória para a prova de Matemática Enem! – https://fuvestibular.com.br/funcao-exponencial-matematica-enem/

Questão 3

(G1 – cftpr 2006) Seja a a raiz positiva e b a raiz negativa da equação 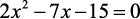. Então o valor de a + 2.b é igual a:

a) – 17/2.

b) 1.

c) – 1.

d) 2.

e) 0.

Dica 3 – O Exame Nacional do Ensino Médio está chegando! Revise sobre Equações Exponenciais para garantir uma boa nota na prova de Matemática Enem – https://fuvestibular.com.br/equacoes-exponenciais-matematica-enem/

Questão 4

(G1 – cftmg 2005) O valor de x na equação [(x + 6)/2] – [(x + 8)/6] = [(x + 10)/4] – [(1 – x)/3] é

a) – 26/5

b) – 2

c) 2

d) 26/5

Questão 5

(Unirio 2003) Marta vai se casar e N amigas suas resolveram comprar-lhe um presente no valor de R$ 300,00, cada uma delas contribuindo com a quantia de X reais. Na hora da compra, entretanto, uma delas desistiu de participar e as outras tiveram, cada uma, um acréscimo de R$ 15,00 na quota inicialmente prevista. Assim, a afirmação correta é:

a) N = 4

b) X = R$ 60,00

c) X = R$ 45,00

d) X = R$ 50,00

e) N = 6

Você consegue resolver estes exercícios? Então resolva e coloque um comentário no post, logo abaixo, explicando o seu raciocínio e apontando a alternativa correta para cada questão. Quem compartilha a resolução de um exercício ganha em dobro: ensina e aprende ao mesmo tempo. Ensinar é uma das melhores formas de aprender!