Antes de você relembrar os cálculos utilizando os logaritmos, vamos ver o que é logaritmo e onde utilizá-lo?
A palavra logaritmo originou-se das palavras gregas Logos (razão) e arithmos (números).
No século XVII, havia dificuldades na elaboração de cálculos devido principalmente às operações de multiplicação, divisão e potenciação.
Burgi, em 1620, e John Napier, em 1614, publicaram as primeiras tabelas de logaritmos, cuja finalidade era a simplificação de cálculos numéricos complicados.
Embora as tabelas de logaritmos não sejam tão usadas atualmente como instrumento de cálculo, os logaritmos são de grande importância em diversas áreas, por exemplo, na medição de terremotos.

Dica 1 – O que mais cai em Matemática nos Vestibulares e no Enem? Veja aqui as melhores dicas: https://fuvestibular.com.br/category/cainaprova/matematica/
O Conceito de Logaritmo:
Para que você compreenda melhor o que é logaritmo, considere uma base positiva e diferente de 1.
Ex: 34 = 81
Ao expoente dessa potência damos o nome de logaritmo. Portanto, 4 é o logaritmo de 81 na base 3.
34 = 81 ⇔ log3 81 = 4
Portanto:
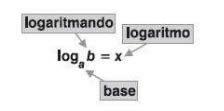
Não podemos sair escrevendo logaritmo de qualquer número em qualquer base. Existem algumas regras para que o logaritmo exista, são as: condições de existência dos logaritmos. Vamos ver quais são essas regras?
Primeira condição:
- b>0
O b – logaritmando – deve ser maior que zero, pois não existe nenhum número que elevado a outro número, o resultado seja zero ou um número negativo. Por exemplo:
Quanto vale log4(-16)?
Ou seja, queremos saber qual o expoente que devemos elevar o número 4 para obtermos -16. Não há valor para este expoente. Chegamos então a um absurdo.
Segunda condição:
- 1 ≠ a >0
A base deve ser um número positivo diferente de 1. Sabe por quê? Vamos ver os exemplos:
Quanto vale log-44?
Ou seja, queremos saber qual o expoente que devemos elevar o número -4 para obtermos 4. Novamente chegamos a um absurdo, não há expoente que faça isso.
Ainda olhando para a base:
Calcule log14 .
Queremos saber qual o expoente que devemos elevar a base 1 para obtermos 4. Como visto no capítulo de potenciação, a base 1 elevada a qualquer expoente resulta 1, ou seja, não existe expoente para a base 1 que resulte 4. Absurdo!
Calcule log14.
Traduzindo, qual o expoente que devemos elevar a base 0 para obtermos 4. Absurdo!
Obs: Note que é dito que a base deve ser um número positivo, ou seja, não pode ser zero também!
Agora que você já relembrou a definição de logaritmo, vamos ver quais são as conseqüências dessa definição? Se liga! Cai no Enem e nos vestibulares de todo Brasil!
a) loga 1 = 0
O logaritmo de 1 é sempre 0, pois a0 = 1.
b) loga a = 1
Quando a base é igual ao logaritmando, o logaritmo é sempre 1, pois a1 = a .
b) loga na = n
O logaritmo de potência da base é sempre o expoente dessa base pois an = an.
d) alog a b = b
Um número a, elevado ao logaritmo de b na base a, é sempre igual a b.
e) loga b = loga c ⇔ b = c
Dois valores são iguais, então, seus logaritmos, na mesma base, também são iguais.
Quer saber mais sobre logaritmos? Então assista a vídeo aula do professor Eduardo Vicente do Descomplica! Nesta o professor explica em 6min 44seg minutos as noções básicas de logaritmos mostrando os nomes dos termos, e, além disso, exercícios são feitos e resolucionados passo a passo para a sua melhor compreensão. Não perca essa oportunidade!
Dica 2 – Complemente os seus estudos para o Exame Nacional do Ensino Médio com esta aula sobre Polinômios que o Blog do Enem preparou para você. Não deixe de conferir! https://fuvestibular.com.br/polinomios-matematica-enem/
Os logaritmos apresentam algumas propriedades operatórias que facilitam as operações que os envolvem. Você lembra quais são? Não se preocupe o blog do Enem te ajuda a relembrar. Fique ligado! Cai no Enem e nos vestibulares de todo Brasil!

Existem também outras propriedades dos logaritmos, que facilitam a vida na hora dos cálculos. O Blog do Enem separou essas propriedades para você tirar de letra na hora da prova. Então veja no quadro abaixo algumas delas:

Dica 3 – Relembre outros assuntos de matemática acessando o nosso blog www.blogdoenem.com.br e gabarite as questões de matemática nas provas dos vestibulares e do Enem.
Agora um desafio para você sobre logaritmos. Vamos lá! Estude e mande super bem na prova do Enem e dos vestibulares de todo Brasil! Coloque a sua resolução num comentário do Facebook no formulário abaixo do post, e compartilhe com as pessoas que estão procurando aprender. Ensinar é a melhor forma de aprender. Você sai ganhando quando ensina, pois nunca mais esquece. Vamos lá?
(CESGRANRIO) Se log10123 = 2,09, o valor de log101,23 é:
a) 0,0209 b) 0,09 c) 0,209 d) 1,09 e) 1,209
Resposta: b

The post Logaritmos: definição e propriedades – Matemática Enem appeared first on Blog do Enem. Tudo sobre Enem, Fies, Sisu, Prouni e Vestibular.