As equações são sentenças matemáticas que contém pelo menos uma incógnita, representada por uma letra, e uma igualdade. Um exemplo bem simples seria:
x + 5 = 12
Queremos saber qual número somado a cinco resulta em doze. É um cálculo facilmente realizado mentalmente, mas vamos realizá-lo passo-a-passo, pois é essencial aprendermos quais são eles para resolvermos as equações mais difíceis. Que tal aprofundar mais no assunto com a coluna da Khan Academy em parceria com o Blog do Enem?
Resolução de equações de uma etapa
As equações de uma etapa podem estar na forma a.x = bou talvezx/a=bsendo a e b números quaisquer e x a incógnita. O número que está multiplicando ou dividindo x passa para o lado direito da igualdade invertendo o sinal de multiplicação ou divisão.
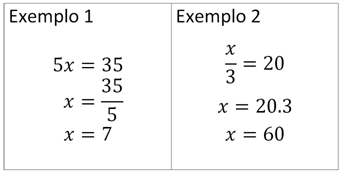
Outra forma possível de equações de uma etapa é a + x = b. Neste caso, a forma de resolver tem o mesmo raciocínio, o número representado por a passa para o lado direito da igualdade invertendo o sinal, se ele for positivo, passa negativo ou vice-versa.
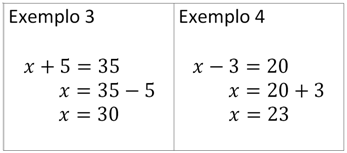
Vídeo-aula: Equações simples:
Exercícios: Aprenda mais com vários exercícios e vídeos do khanacademy.org https://pt.khanacademy.org/math/cc-seventh-grade-math/cc-7th-variables-expressions
Resolução de equações de duas etapas
É claro que nem todas as equações podem ser tão facilmente resolvidas nos vestibulares e no ENEM. As equações de duas etapas são bem mais comuns, elas estão na forma ax + b = c ou x/a +b=c sendo a, b e c números e x a variável. Neste caso, devemos seguir passando para o lado direito primeiro os números que estão somando ou subtraindo, lembre-se que eles invertem o sinal neste processo, depois você passa para o lado direito os números que estão multiplicando ou dividindo a incógnita também não esquecendo de inverter o sinal também.

Vídeo-aula: Equações 2:
Exercícios: Aprenda mais com vários exercícios e vídeos do khanacademy.org
Dica: Revise o método de resolução de equações do segundo grau: https://fuvestibular.com.br/equacao-polinomial-segundo-grau-matematica-enem/
Desafios
1) (ENEM 2011) O saldo de contratações no mercado formal no setor varejista da região metropolitana de São Paulo registrou alta. Comparando as contratações deste setor no mês de fevereiro com as de janeiro deste ano, houve incremento de 4 300 vagas no setor, totalizando 880 605 trabalhadores com carteira assinada.
Disponível em: http://www.folha.uol.com.br. Acesso em: 26 abr. 2010 (adaptado).
Suponha que o incremento de trabalhadores no setor varejista seja sempre o mesmo nos seis primeiros meses do ano.
Considerando-se que y e x representam, respectivamente, as quantidades de trabalhadores no setor varejista e os meses, janeiro sendo o primeiro, fevereiro, o segundo, e assim por diante, a expressão algébrica que relaciona essas quantidades nesses meses é
A) y = 4 300x
B) y = 884 905x
C) y = 872 005 + 4 300x
D) y = 876 305 + 4 300x
E) y = 880 605 + 4 300x
2) (ENEM 2011) O prefeito de uma cidade deseja construir uma rodovia para dar acesso a outro município. Para isso, foi aberta uma licitação na qual concorreram duas empresas.
A primeira cobrou R$ 100 000,00 por km construído (n), acrescidos de um valor fixo de R$ 350 000,00, enquanto a segunda cobrou R$ 120 000,00 por km construído (n), acrescidos de um valor fixo de R$ 150 000,00. As duas empresas apresentam o mesmo padrão de qualidade dos serviços prestados, mas apenas uma delas poderá ser contratada.
Do ponto de vista econômico, qual equação possibilitaria encontrar a extensão da rodovia que tornaria indiferente para a prefeitura escolher qualquer uma das propostas apresentadas?
A) 100n + 350 = 120n + 150
B) 100n + 150 = 120n + 350
C) 100(n + 350) = 120(n + 150)
D) 100(n + 350 000) = 120(n + 150 000)
E) 350(n + 100 000) = 150(n + 120 000)
Gabarito
1) C; 2)A
Autoria de Alexsandro Sunaga https://www.facebook.com/alexsandro.sunaga
Este post é resultado da parceria da Fundação Lemann com o Blog do Enem – www.fundacaolemann.org.br
The post Perca o medo de resolver equações – Matemática Enem appeared first on Blog do Enem. Tudo sobre Enem, Fies, Sisu, Prouni e Vestibular.