Sistemas Lineares: Resolvendo Sistema de Equações Lineares

Um “sistema” de equações é um conjunto ou coleção de equações com as quais você lida “sistematicamente” com todas juntas ao mesmo tempo. Equações lineares (aquelas nas quais os gráfico representantes são linhas retas) são mais simples do que as equações não-lineares, e a forma de sistema linear mais simples é a de um com duas equações e duas variáveis.

Vamos considerar sistemas com equações lineares. Por exemplo, considere a seguinte equação:

y = 3x – 5

A solução para esta equação são quaisquer pontos x, y que satisfaçam a equação. Então, (2, 1) é uma solução porque, atribuindo 2 para o valor de x nos temos:

3x – 5 =
- 3(2) – 5 =
  - 6 – 5 =
    - 1 = y

Por outro lado, (1, 2) não seria uma solução válida, uma vez que, ao substituir o valor de x:

3x – 5 =
- 3(1) – 5 =
  - 3 – 5 =
    - –2

… o que não se iguala ao valor de y (o qual era 2, para este ponto). E é claro que, em termos práticos, não encontramos as as soluções para este sistema de equações escolhendo pontos aleatórios, conectando-os, e verificando se eles “satisfaziam” as equações.

Ao invés disto, escolhemos os valores de x e, em seguida, calculamos os valores de y correspondentes. E usamos o mesmo procedimento para representar graficamente a equação. Isto aponta um facto importante:

Cada ponto no gráfico é uma solução para a equação, e qualquer solução para a equação é um ponto no gráfico.

Representação Gráfica da Resolução de Sistemas

Agora, considere o seguinte sistema de duas variáveis de equações lineares:

y = 3x – 2
y = –x – 6

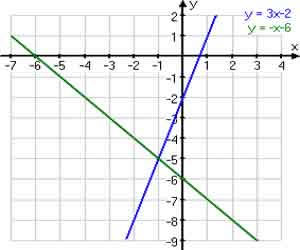
Uma vez que as duas equações anteriores estão em um sistema, nós lidamos com elas em conjunto, ao mesmo tempo. Em particular, podemos representá-las graficamente juntas no mesmo sistema de eixos, como aqui:

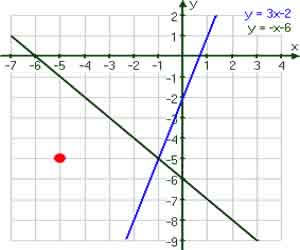
A solução para uma única equação é qualquer ponto que se encontre sobre a reta para esta equação. Uma solução de um sistema de equações é qualquer ponto que se encontre em ambas as retas do sistema. Por exemplo, o ponto vermelho à direita não é uma solução para o sistema, uma vez que não está em qualquer uma das retas:

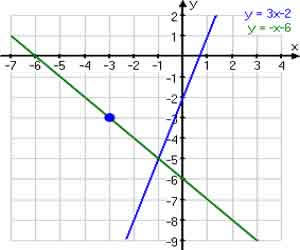
O ponto azul à direita não é uma solução para o sistema também, uma vez que se encontra em apenas uma das retas, não em ambas:

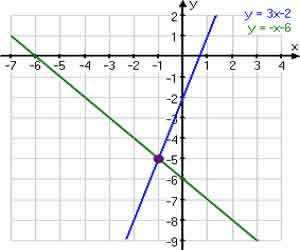
O ponto de roxo à direita é uma solução para o sistema, uma vez que se encontra em ambas as retas:

Em particular, este ponto roxo marca a interseção das duas retas. Uma vez que este ponto está em ambas as retas, ele portanto resolve ambas as equações, de modo que resolve todo o sistema.

E esta relação é sempre verdadeiro: Para sistemas de equações, “soluções” serão sempre os “cruzamentos” de retas, as interseções. Você pode confirmar a solução através de substituir os valores das coordenadas no sistema de equações, e confirmar que a solução satisfaz cada uma das equações.

Exemplos:

Determine se qualquer um dos pontos (-1, -5) e (0, -2) é uma solução para o sistema de equações:
- y = 3x – 2
- y = –x – 6

Para verificar as possíveis soluções dadas, você só precisa substituir os valores das coordenadas de x e de y nas equações, e verificar para confirmar se elas satisfazem a equação.

verificação de (-1, -5) em y = 3x – 2:
- (–5) = 3(–1) – 2
  –5 = –3 – 2
  –5 = –5 (satisfaz a equação)
verificação de (-1, -5) em y = –x – 6:
- (–5) = –(–1) – 6
  –5 = 1 – 6
  –5 = –5 (satisfaz a equação)

Uma vez que o ponto dado satisfaz ambas as equações, ele é uma solução para o sistema. Agora vamos verificar o outro ponto:

verificação de (0, –2) em y = 3x – 2:
- (–2) = 3(0) – 2
  –2 = 0 – 2
  –2 = –2 (satisfaz a equação)

Então, a solução satisfaz uma das equações. Mas para resolver o sistema, ela deve equivaler a igualdade em ambas as equações. Então continuando a verificação: