Conta de Mais: Propriedades da Adição +

O conhecimento das propriedades da operação Aritmética elementar de soma é um fundamento essencial da matemática básica, sendo um conteúdo normalmente abrangido no ensino fundamental.

Conheça, ou revise, abaixo as propriedades básicas da conta de mais, ou da adição:

Associativa

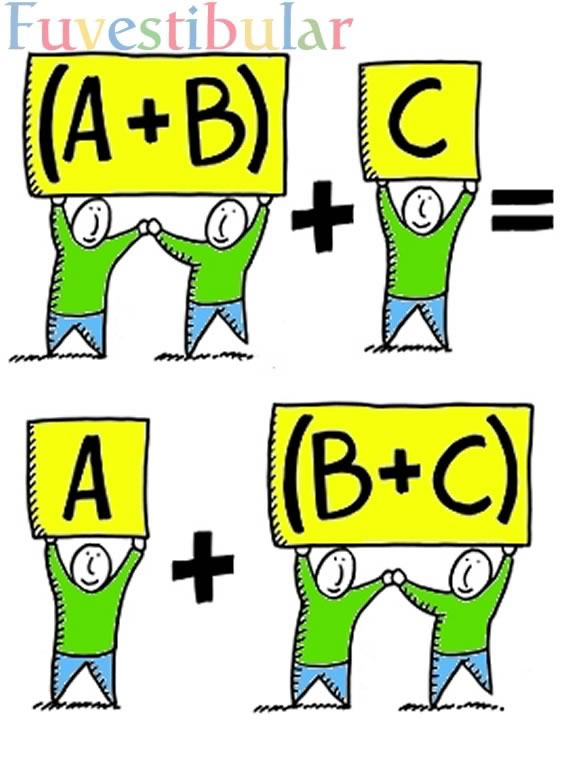
Uma das propriedades da adição é a associativa, a qual é aplicável quando tentamos definir a ordem de sucessivas somas.

Por exemplo, na soma:

a + b + c

Qual seria o mais correto de ser definido como uma ordem para realizar as somas:

(a + b) + c …?

ou…

a + (b + c) …?

A propriedade associativa da soma irá nos dizer que qualquer escolha na definição da ordem das parcelas é irrelevante. Pois que, para qualquer soma de N parcelas, o resultado será sempre o mesmo independentemente de como associarmos a ordem da soma destas N parcelas.

Ou seja:

(a + b) + c = a + (b + c)

E como a multiplicação é apenas um tipo especial de soma, ela compartilha de mesma propriedade.

Porém nas operações de subtração e divisão a ordem das operações é determinante na expressão do resultado.

Neutro

Há um número, e somente um único, que quando adicionado a qualquer outro número não o altera: este número é o zero (0). Também conhecido como elemento neutro da adição ou identidade aditiva.

Simbolicamente, expressa como:

a + 0 = 0 + a = a, para todo a ∈ $\mathbb{Z}$

Oposto

Anulação ou Número Aditivo Inverso é o mesmo que a identidade Inversa: é qualquer número que, quando adicionado a um número N, resultará em zero.

Para cada inteiro N existe um único elemento que chamaremos de oposto de a e indicaramos por -N, tal que:

N + (-N) = 0.

Assim, em geral, o aditivo inverso (oposto) de N é -N.

Comutativa

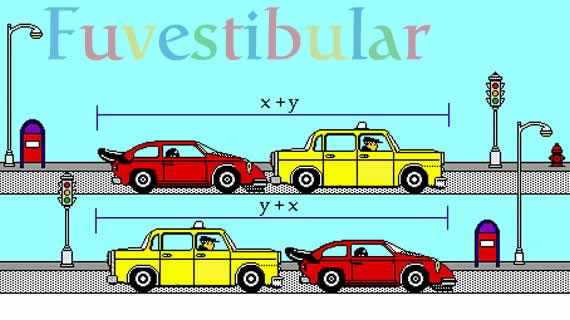
A ordem das parcelas não altera a soma.

A adição, ou conta de mais, é uma operação matemática comutativa. O que, em outras palavras, significa dizer que: podemos * comutar indiferentemente as parcelas de uma soma sem que seu resultado se altere.

(*)comutar= Trocar; mudar; substituir; permutar; variar.

Simbolicamente, representa-se esta propriedade da adição da seguinte maneira:

a + b = b + a

Esta é a lei comutativa da soma, a qual também é válida para a operação de multiplicação uma vez que a conta de vezes é nada mais do que uma SOMA.

Qualquer multiplicação é uma soma de 2 ou mais fatores iguais, e como tal é uma operação subordinada a propriedade comutativa.

No entanto, subtrações e divisões não são operações matemáticas subordinadas a esta “lei” ou propriedade matemática.

Fechamento

A soma de dois números reais será sempre um número real.

Sucessores

Dentro do contexto do universo dos números inteiros, a adição de: + 1 desempenha uma função muito importante:

Para qualquer número inteiro a, o inteiro (a + 1) será o menor número inteiro maior do que a

Este número é aquele conhecido como Sucessor de a.

Esta propriedade gera uma importante consequência na operação matemática de soma:

Na soma de a + b
- b é um número tal que exprime, através da quantidade que seu algarismo representa, a ordem de sucessão de a
  - Exemplos de números para b:
    - a + 1 = ao primeiro sucessor de a
    - a + 2 = ao segundo sucessor de a
    - a + 99 = nonagésimo nono sucessor de a

Neste sentido, toda soma é uma sucessão numérica.

Unidades Homogêneas e Heterogêneas

Para ser possível somar quantidades físicas com unidades de medida estabelecidas, elas precisam estar em unidades comuns entre elas.

Por exemplo, se uma parede de 2 metros for estendida em 50 centímetros, a soma será simples: 2,5 metros, desde que centímetro é uma unidade de medida derivada da unidade metro (um sub-múltiplo dela).

Já por outro lado, tentar somar 50 centímetros a 50 polegadas quadradas não faz qualquer sentido, desde que estas unidades de medida são insociáveis.

É dito que para que possamos somar duas ou mais quantidades, elas precisam ser quantidades homogêneas, ou seja: Quantidades de uma mesma “espécie”.

O contrário disto são as unidades heterogêneas, quantidades que representam quantidades de coisas diferentes e que como consequência não podem se associar em uma soma.

Propriedades na prática na Efetuação de Cálculos Mentais

As duas propriedades anteriores embora pareçam muito simples, são muito eficazes e nos ajudam a fazer cálculos mais prontamente.

Digamos que precisamos calcular a soma:

23 +65 +12 +35

Aqui podemos computar primeiro 65 +35 usando as duas propriedades descritas acima e, em seguida, calcular 23 + 12. Isto torna mais fácil somar e realizar cálculos mentais, ou seja: