Decomposição em Fatores Primos

Decompor um dado número qualquer em seus fatores primos significa o escrever na forma do produto de seus fatores (ou divisores) primos.

Se conceitualmente pode não soar a coisa mais simples do mundo, não se preocupe. Pois é uma das, e na prática o processo é bastante simples:

Para efetuar a decomposição de um número em seus fatores primos, procedemos com a Árvore de fatoração. Dado um número n qualquer, ela consistirá no seguinte processo:

• Encontrar o menor número primo divisor de n; No nosso exemplo, n = 75.

• Assim, o menor número primo que podemos considerar é o 2. Porém, verificando se 2 pode ser divisor de 75 denotamos que não se pode dividir 75 igualmente por 2.
• Passando para o imediatamente próximo número primo, chegamos ao 3. E verificando a possibilidade dele dividir 75, damos conta de que 75 é divisível por 3. Em outras palavras: 3 vezes algum número é igual a 75.

• Nos resta encontrar o número “X” que vezes 3 =75, o que equivale a resolver:
  • x.3=75
    • x=75/3
      • x=25
• De modo que encontramos uma possível fatoração do número 75 em números primos:

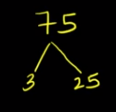
• No entanto, desejamos encontrar a mínima fatoração. E apesar de não podermos fator 3 em fatores primos menores, podemos isto fazer com relação ao número 25.
• Não podemos fatorar 25 por 2, nem por 3, (quatro não é número primo), mas podemos por 5:

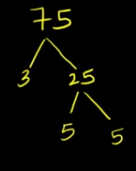
• Chegamos a menor fatoração do 25, do mesmo modo que com o 3, não podemos fatorar o 5 em fatores primos menores. E assim chegamos ao fim de nossa decomposição do número 75 em seus fatores primos, que é:

75=3 x 5 x 5